It is He who sits above the circle of the earth, and its inhabitants are like grasshoppers, who stretches out the heavens like a curtain, and spreads them out like a tent to dwell in. (Isaiah 40:22)

When God stretched out the heavens, did He stretch out space itself? If so, what exactly is space? Is it a field, a fabric, or a structure we can measure?

Have you ever stood by a pond and tossed stones into the water, or stood on the seashore and watched waves crash against the rocks? Both are examples from everyday life of wave phenomena. The impact of the stone on the water causes waves to radiate from where the stone impacted the water. Similarly, our ability to listen to a Mozart symphony, a bird’s song, or conversations with those around us depends on waves created in the air by vibrations of matter.

Earthquakes generate waves within the earth, p-waves that propagate along the direction of the wave, and s-waves that propagate transverse (or perpendicular) to the direction of the wave. All these are examples of what are generally classified as mechanical waves, i.e., waves that result from the oscillation (rhythmic movement) of matter. This type of movement transfers energy through space occupied by matter.

A second general wave classification is the electromagnetic wave, which does not require the presence of matter in order to transfer energy through space. Rather, it is the result of vibrations in the electrical and magnetic fields. Electromagnetic waves, unlike mechanical waves, can propagate through the apparent vacuum of outer space (i.e., space not occupied by matter) as well as through matter itself. When propagating through outer space, electromagnetic waves vibrate in planes perpendicular to the direction of motion. These are transverse waves. Electromagnetic waves familiar to our everyday experience include visible light, microwaves, and radio waves. Less familiar are gamma rays from radioisotope decay and high-energy cosmic phenomena in the earth’s upper atmosphere.

A third general wave classification is the gravitational wave. These waves are literally “ripples” (see Figure 1) in the space-time continuum caused by some of the most violent and energetic processes in our universe. This type of wave oscillates in the transverse plane like an electromagnetic wave, but its possible polarization states are not described by a transverse vector like electromagnetic waves but are rather described by a transverse second rank tensor. Analogous with electromagnetic waves, which are generated by the acceleration of electrical charges, gravitational waves are generated by the acceleration of massive objects, and these waves are believed to travel at the speed of light.

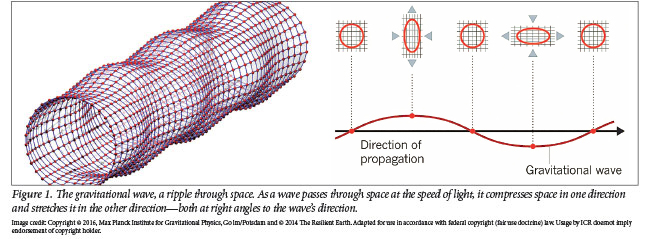
Since the early 20th century when Albert Einstein formulated his general relativity hypothesis, the possibility for gravitational waves propagating through the space-time continuum has been a topic of great interest and much discussion in mainstream science. The first observational evidence for the veracity of general relativity came from an expedition led by Sir Arthur Eddington to observe the total solar eclipse of May 29, 1919. Eddington confirmed the general relativity prediction that starlight would be deflected by the sun’s gravity.

Indirect evidence supporting a prediction of general relativity was observed and documented by astrophysicists Russell Hulse and Joseph Taylor in 1974.¹ They discovered that the orbital decay of a binary pulsar they were studying matched the predictions of general relativity. Recently, another prediction of general relativity that gravity should propagate energy via wave phenomena when massive objects are accelerated was experimentally observed—thus adding more supporting evidence to the general relativity hypothesis and creating much excitement in the scientific community.^2-4

All waves have four characteristics that describe their propagation through the space-time continuum.

1. The first is amplitude (h), which describes the size or strength of a given wave. If the wave is passing through a medium, it describes the stretching or squeezing of that medium as the wave passes through it.
2. A second characteristic is frequency (ν), which describes how the wave oscillates in the medium it passes through.
3. Wavelength (λ) is the third characteristic. It’s the spatial distance between maximum points of stretch or compression in the wave.
4. Finally, speed (v) is the velocity with which a given point on the wave travels through space.

The last three characteristics are related, and this relation is expressed as v = λν.

Gravitational waves have some characteristics that are similar to those of electromagnetic waves. They can propagate through an apparent vacuum, they travel at the speed of light, and they are transverse waves in structure. In fact, Henri Poincaré first suggested in 1905 that accelerating masses should produce gravitational waves much like accelerating electrical charges produce electromagnetic waves. Gravitational waves are constantly passing through Earth, but the amplitudes of even the strongest are minuscule when they arrive here, and thus they are extremely difficult to detect.

For example, the gravitational waves from the cataclysmic final merger of GW150914 (a binary black hole) reached Earth, after traveling over a billion light-years, as a ripple in space-time that changed the length of the 4-km LIGO (Laser Interferometer Gravitational-Wave Observatory) arm by only one ten-thousandth the width of a proton—proportionally equivalent to changing the distance from our solar system to the nearest star by one hair’s width. This is the measurement problem that LIGO faced and solved on September 15, 2015, when black holes having solar masses⁵ of 36 and 29 were observed merging into a black hole with a solar mass of 62 at an approximate spatial distance of 1.3 billion light-years. This ultra-precise measurement marked a phenomenal scientific achievement.

Several questions arise from this observation. How much energy was released by the massive merger, and what was the frequency and wavelength of the gravitational wave? First, we can estimate the energy released by calculating the energy equivalent of the missing mass after the merger. Before the merger, the total mass of both black holes was 36 + 29 solar masses, or approximately 65 solar masses. After the merger, a single black hole with a solar mass of 62 remained. What happened to the missing three solar masses? It was turned into the energy transported by the subsequent gravitational wave throughout the universe.

Using Einstein’s famous equation E = mc², where E is the energy equivalent of the missing mass and c is the speed of light, we can estimate the energy released as gravitational waves.

E = mc² = 3 × (1.989 × 10³⁰kg)(2.99792 × 10⁸m/sec.)²
        ≈ 5.4 × 10⁴⁷ kg m²/sec² = 5.4 × 10⁴⁷ joules

This is approximately 10²¹ more energy than the total electromagnetic radiation given off by our sun.

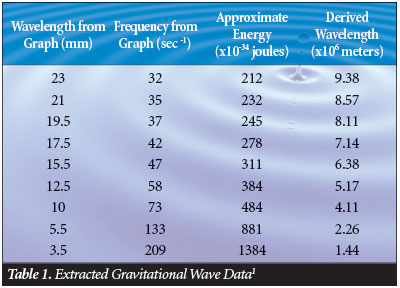
According to classical general relativity, gravitational waves propagate with a velocity equal to the speed of light, i.e., v = c. This allows us to make some interesting inferences concerning the frequency and wavelength of the observed black-hole merger. We can extrapolate the data presented in reference 1, Figure 12, into a table (Table 1) from which we can estimate the frequency and wavelength of the gravitational wave generated at the instant of merger. The first thing to note about Table 1 is that the wavelength extracted directly from the experimental data would be in great error since c = λν. This is because the arms of the LIGO detector will vibrate with the frequency of the gravitational wave but the wavelength recorded is a function of the experimental apparatus and not the gravitational wave per se. So, if we substitute the Table 1 frequency into the c = λν formula and solve for λ we get:

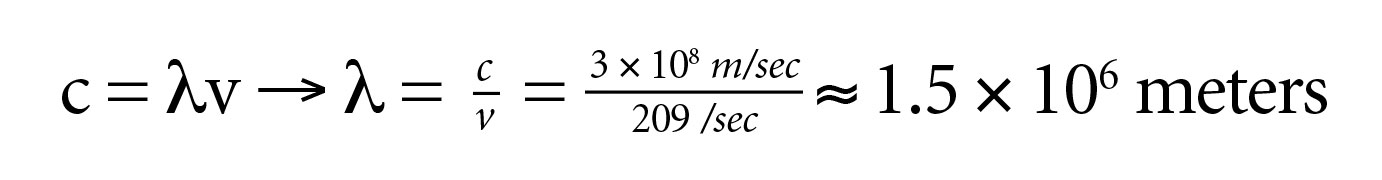
Thus, the approximate wavelength for the gravitational wave generated by the black hole merger is 1,500 kilometers.

While gravitational waves possess many properties similar to electromagnetic waves, they are an intrinsically different type of phenomena. If gravitational waves possess a quantum particle (the graviton) as its force carrier, it is expected to be massless (i.e., the associated force has infinite range), and unlike the electromagnetic photon it is believed to be a spin-2 boson.⁶ However, to date, no “force carrying” particle has been observed as a mediator of gravitational interactions, and therefore no reconciliation currently exists between general relativity theory and the Standard Model that describes all other fundamental forces. This is still a substantial mystery.

Many other questions remain. Scientists still do not understand all the nuances of space and time. So what exactly is this space-time continuum that oscillates like an electric quadrapole when mass is accelerated? How can gravitational waves transport massive amounts of energy through an apparent vacuum? In the biblical record, the Lord declared He stretched out the heavens like a curtain.⁷ Does this indicate that the apparent vacuum of outer space actually has a structure, fabric, or field we have yet to discover—that even empty space is “something” rather than “nothing”? Does the space-time continuum provide a transport mechanism for the natural phenomena we observe such as gravitational waves? This recent scientific discovery seems to confirm the Bible’s implication that space is a real entity with measurable properties.

God designed each aspect of reality to function in very specific ways that sustain life on Earth, and we are only beginning to understand the space-time continuum—the curtain God stretched out in the beginning.

References

1. Taylor, J. H. and J. M. Weisberg. 1982. A new test of general relativity-Gravitational radiation and the binary pulsar PSR 1913+16. Astrophysical Journal. 253 (2): 908-920.
2. Abbott, B. P. et al. 2016. Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters. 116 (6): 061102.
3. Abbott, B. P. et al. 2016. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Physical Review Letters. 116 (24): 241103.
4. Ohanian, H. C. and R. Ruffini. 1994. Gravitation and Spacetime, 2nd ed. New York: W. W. Norton & Company.
5. A solar mass is simply the mass of our solar system’s sun—i.e., 1.989 x 10³⁰ kilograms. Astronomers typically express the estimated masses of very large objects in the universe in multiples of this number.
6. In general relativity, the stress-energy tensor T^αβ describing the gravitational field is generally a second order tensor (meaning it has magnitude and two directions rather than a magnitude and one direction as for a first order tensor, or what we generally know as a vector). The lowest allowed multipole solutions to the linearized general relativity equations is the quadrapole (l = 2). Monopole solutions are forbidden as a result of mass conservation, and dipole solutions are absent as a result of momentum conservation. Thus, the lowest order solutions to the general relativity equations (gravitational waves) must be second order tensors—i.e., spin 2 solutions.
7. Psalm 104:2; Job 9:8; 26:7; Isaiah 44:24; 45:12; 51:13; Jeremiah 10:12; Zechariah 12:1.

* Dr. Cupps is Research Associate at the Institute for Creation Research and earned his Ph.D. in nuclear physics at Indiana University-Bloomington.