The secret things belong unto the Lord our God: but those things which are revealed belong unto us and to our children forever, that we may do the words of this law. (Deuteronomy 29:29)

Editor’s note: We’ve received a wide range of responses to Dr. Vernon Cupps’ recent radioactive dating Impact articles. Most readers appreciate the hard science, but many have struggled with the equations. The purpose of this series is to demonstrate in no uncertain terms that these dating methods do not prove that Earth is millions or billions of years old, as is often reported. To provide context for Part 4, below is a summary of the first three articles—all are available online.

Part 1: Clocks in Rocks?

There are significant problems with radioisotope dating in general. The critical closed-system assumption is not realistic—no system can remain unaffected by its environment over millions of years. Evolutionists appeal to radioactive dating because it appears to confirm the deep time their models demand, but the actual data don’t match the evolutionary model.

Part 2: The Iconic Isochron

The isochron dating method gives erroneous ages for rock formations of known age. Specifically, rocks gathered from recently erupted Mt. Ngauruhoe in New Zealand gave isochron dates of between 270,000 years and 3.9 billion years—from rocks known to be less than 60 years old! The isochron model is only a hypothesis. Models, no matter how elegant their mathematics, are only as good as their assumptions and how well they reproduce reality through observation and experimental data. The scientific method simply does not allow isochron-model dating to be presented as scientific fact.

Part 3: The Noble Clock

In addition to the unreasonable assumptions that form an integral part of all three K-Ar (potassium-argon) dating methods, there are many examples in which the methods give erroneous dates. The K-Ar model does not meet even the basic criteria of a scientific hypothesis. Researchers who use these dating methods to conclude that rock-sample dates are evidence of a millions- or billions-year-old Earth are not using a legitimate scientific method. The potassium-argon dating method—once heralded as a solid scientific method—has proven to be unreliable.

______________

Using rubidium (Rb) decay as a clock to date minerals was first suggested by Otto Hahn and Ernst Walling in 1938. Five years later, Hahn performed the first age determination using this method.

Like potassium (K), rubidium is an alkali metal and therefore chemically behaves much like potassium. Physically, it has an ionic radius of 1.48 Å, which is close to potassium’s (1.33 Å) and therefore should move within a crystal structure in a similar manner. This allows rubidium to readily substitute for potassium in all K-bearing minerals.

Determining the half-life of Rb presents scientists with a challenge for two reasons. First is the extremely long half-life of Rb, and second is because Rb beta decays with a relatively small energy of 275 keV. During beta decay, the decay energy is shared; thus, the emitted beta particle has a spectrum of energies rather than a single unique energy, making direct detection of the beta particle difficult. From 1964 through 2012, seven attempts were made to directly measure the half-life of Rb. The results of these measurements have varied from 4.77 ± 0.10 x 10¹⁰ yrs. in 1964 to 4.967 ± 0.032 x 10¹⁰ yrs. in 2003. A value of 4.88 x 10¹⁰ yrs. is used by Gunter Faure and Teresa Mensing³ and is the current value recommended by the Union of Geological Sciences. Whether this decrease is real or simply due to better measurement techniques remains uncertain. In any case, there is some uncertainty in one of the critical parameters used by isochron dating models of Rb decay.

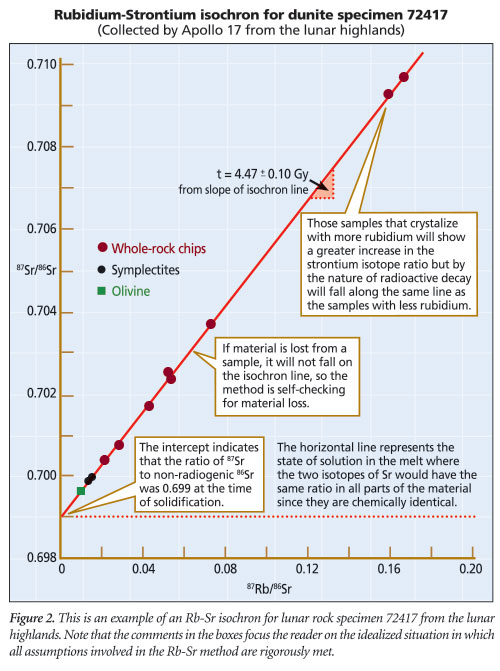
A little-advertised characteristic of rubidium-containing minerals is that they are moderately rare in nature.⁴ When they do occur in rock samples, they are usually in such small amounts that they cannot be seen without a microscope (see Figure 1). Therefore, separating the element from the rock sample is difficult. This makes mineral isochrons for the Rb-Sr decay sequence rare and is the reason most isochrons in the literature for this dating method use whole-rock isochrons.

What are the critical assumptions that go into this dating method? One basic assumption that was outlined in a previous Acts & Facts article⁵ —constant decay rates—is equally invalid for this dating method.

A second basic assumption, that the rock suite remains a truly closed system over millions of years, is simply not reasonable since both Rb and Sr are mobile and easily transported via diffusion or hydrothermal action in a rock suite. In addition, ⁸⁶Sr has a high neutron capture cross-section of 190 barns for thermal neutrons and thus can produce ⁸⁷Sr independent of the presence of ⁸⁷Rb; it would not take much ⁸⁷Sr produced in this manner to seriously skew the age calculated by this method. The closed-system assumption probably does not hold for this dating method.

The third basic assumption is that the initial concentration of the daughter isotope can be derived by applying the isochron method to a group of rock samples in the present time. There are a number of critical secondary assumptions hidden in this third basic assumption:

1. The rock formation was sufficiently mixed that m = 0 can be assumed to be its initial condition.
2. ⁸⁷Sr can only be generated by the radioactive decay of ⁸⁷Rb during the entire life of the rock formation.
3. ⁸⁷Rb nuclei are only removed from the rock formation via their decay to ⁸⁷Sr.
4. The number of ⁸⁶Sr atoms/unit weight of the rock remains constant in time. This is critical since such small amounts of ⁸⁷Sr are involved.
5. The temperature of the rock formation, or any part of it, has never gone above the closure temperature for strontium or rubidium-containing minerals. This could result in the inheritance of isotopic ratios from heterogeneous source rock.

Assumptions 2 through 5 are related to the closed-system assumption and come into play in the Rb-Sr isochron methodology through assumptions made in deriving the time evolving linear equation fundamental to the method. All three isotopes used in this method—⁸⁶Sr, ⁸⁷Sr, and ⁸⁷Rb—can be produced in a given rock suite by cosmogenic processes. For example, ⁸⁷Sr can not only be produced by the neutron capture reaction on ⁸⁶Sr, it can also be produced by the (n,α) nuclear reaction on ⁹⁰Zr. This reaction has a much smaller cross-section (~ 25 X 10^-3 barns) than the (n,γ) reaction on ⁸⁶Sr, but even small amounts of ⁸⁷Sr generated by processes other than decay of ⁸⁷Rb will negate one of the basic assumptions upon which the whole methodology of Rb-Sr isochrons are built. ⁸⁷Rb can be converted to ⁸⁸Rb through the (n,γ) reaction (~ 310 barn cross-section), thus removing it from the rock matrix without decay to ⁸⁷Sr.

If the temperature of the rock formation goes above the closure temperature, then the strontium and rubidium atoms are essentially free to move within the rock formation and interact with their environment, thus disrupting the presumed initial isotope ratios. So essentially, this methodology assumes that all ⁸⁷Sr found in a rock formation above a level consistent with a baseline ratio to ⁸⁶Sr is generated by radioactive decay with no allowance for ⁸⁶Sr, ⁸⁷Sr, and ⁸⁷Rb being primordially present or generated by other processes.

Assumption 1 is directly related to our old friend the homogeneous assumption. As previously discussed,⁵ this assumption is critically flawed. If we assume that the rock formation cooled slowly enough for all elements within it to reach chemical and physical equilibrium, then the whole-rock samples of the formation should have the same concentrations of each element in a given sample. This applies not only to strontium but also to rubidium. Therefore, for a true isochron, the whole-rock samples should all fall at a single point, not a series of points. A single mineral should exhibit the same behavior. We can then conclude that an isochron can only be constructed from a group of different, separated minerals in the same rock formation that formed at the same time. Unfortunately, Faure points out that model dates derived from the analysis of separated minerals are generally unreliable.⁶ So, as pointed out above, most of the Rb-Sr isochrons in the literature are whole-rock isochrons. The fact that we can construct linear relationships from samples of current rock formations could just as easily have arisen from mixing that occurred as the rock solidified than from a reliable clock frozen in time for millions or billions of years.

So what does the observable evidence say about the Rb-Sr isochron dating method? New Zealand’s Mt. Ngauruhoe example gave a Rb-Sr isochron date of over 133 million years to rock known to be less than 60 years old.⁷ Another example of rock from east Africa’s Virunga Toro-Ankole region yielded an Rb-Sr isochron model age of 773 million years for rock known to be younger than five million years even from the secular viewpoint.⁸

Whole-rock and mineral Rb-Sr isochrons of granitic rocks from the northern Scottish Highland’s Carn Chuinneag complex give ages of 548 ± 10 million years and 403 ± 5 million years respectively.⁹ This is about a 150 million-year difference—which one is correct?

Dr. Steve Austin dated the Grand Canyon Cardenas Basalt at between 0.98 ± 0.06 and 1.10 ± 0.05 billion years using the Rb-Sr isochron dating model. He also dated the Grand Canyon Uinkaret Plateau basaltic rocks at between 1.27 ± 0.04 and 1.39 ± 0.03 billion years using the Rb-Sr dating method.¹⁰ Other than the fact that the range of dates does not overlap within the stated error bars, it is interesting that the highest rock strata are dated to be at least eight million years older than the base level rock strata. This conflicts with the long-standing axiom of rock strata being indicative of geological ages.

Therefore, the assumptions the Rb-Sr isochron dating method is based on do not seem to be reasonable, and the predictions of this model do not coincide with observations. What can we conclude? Can we believe a model that does not reproduce the known ages of rocks is valid for dating rocks of unknown ages?

The most important thing we must remember about radioisotope dating is that the present-day measurements and observations are valid scientific facts. What is not valid scientific fact is the extrapolation of those measurements and observations into the past. If the many assumptions that go into extrapolating current measurements into the past are reasonable, and if they are verified by current observations, then they can, at best, be considered rational approximations to past events. But if the assumptions are not wholly reasonable and verifiable, then they cannot be used as reliable scientific dating methods. Evolutionists may claim that radioactive dating methods prove the earth’s strata to be millions of years old, but they won’t tell you that those methods are built on a house of cards that cannot bear the weight of scientific scrutiny.

Click here to read “Radioactive Dating, Part 1.” Click here for Part 2. Click here for Part 3.

Click here to read "Radioactive Dating, Part 5."

References

1. ICRP. 1983. Radionuclide Transformations: Energy and Intensity of Emissions. ICRP Publication 38. Annals of the IRCP. 11-13.
2. Faure, G. 1986. Principles of Isotope Geology, 2nd ed. New York: John Wiley & Sons, 119.
3. Faure, G. and T. M. Mensing. 2005. Isotopes: Principles and Applications, 3rd ed. New York: John Wiley & Sons, 77.
4. Rubidium is found in easily detectable quantities only in the minerals ramanite, rubicline (see Figure 1), and voloshinite. Typically it takes EDS (energy dispersive spectroscopy) to detect even their presence in these crystals. This is why most Rb-Sr isochrons are of the whole-rock type.
5. Cupps, V. R. 2014. Clocks in Rocks? Radioactive Dating, Part 1. Acts & Facts. 43 (10): 10-13.
6. Faure, Principles of Isotope Geology, 124.
7. Snelling, A. A. 2003. The Relevance of Rb-Sr, Sm-Nd, and Pb-Pb Isotope Systematics to Elucidation of the Genesis and History of Recent Andesite Flows at Mt. Ngauruhoe, New Zealand, and the Implications for Radioisotopic Dating. Proceedings of the Fifth International Conference on Creationism. R. L. Ivey, Jr., ed. Pittsburgh, PA: Creation Science Fellowship, 285-303.
8. Faure, Principles of Isotope Geology, 146-147.
9. Ibid, 127.
10. Austin, S. A. 1994. Grand Canyon: Monument to Catastrophe. Santee, CA: Institute for Creation Research, 123,125.

* Dr. Cupps is Research Associate at the Institute for Creation Research and received his Ph.D. in nuclear physics from Indiana University-Bloomington.